無理数 記号 257283-有理数 無理数 記号

 · 正の数と負の数 22 文字と式（中学） 19 一次方程式 23 比例と反比例（中学） 16 平面図形（中学） 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9基本的に記号" ≡ "は数式や関数を定義するときに用いるが, この記号では左辺と右辺のどちらが定義される側かの判別がつかないこともある13 無理数の連分数展開 ここでは一般の無理数!を連分数で表すことを考えよう．まず記号を準備し ておく．今までの連分数展開の書き方を拡張して任意の実数tに対して a0 1 a1 1 an

べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ

有理数 無理数 記号

有理数 無理数 記号-ただし、n は自然数（1以上の整数）、i は虚数記号。 問題終 雑談 上記のような、虚数部の記号がプラスかマイナスか、だけが異なる2つの複素数を共役複素数、または、複素共役という。$\sqrt{2}$ が無理数であることのいろいろな証明方法を紹介します．すべて，高校までの数学で理解できるものです． 教科書に乗っている証明 まずは，教科書に乗っている標準的な証明を紹介します．$\sqrt{2}$ を有理数と仮定して， 互いに素 な $2$ つの整数の比で表し，矛盾を示します．

大学数学 集合 数学 大学 に関する質問 勉強質問サイト

もう一つ身近な無理数の例に平方根があります。 √で表される数字です。 もちろん、√の全ての数字が無理数ではなく、割り切れない（√が外せない）数字が無理数になります。 このように有理数か無理数かは、分数で表せるかどうかで判断できます。 有理数を表す記号性質2a;bが有理数のとき，ab 2 = 0ならばa = b = 0 であることを証明せよ．ただし， √ 2は無理数である(5)． 記号化 「xが有理数である」はx ∈ Q，「xが無理数である」は x ̸∈Q と記号化できるので，求める記号化は 2 ̸∈Q;a ∈ Q∧b ∈ Q → ab 2 = 0 ⊃ a = 0∧b = 0 である． SNK に基づく証明で表します．なお，これらは数学を研究する上でも一般的な記号です． 数学的な「個数」 まずは，数学的に「個数が等しい」というのをどのように考えるかを説明します． 有限集合の濃度(個数)

無理数を表す記号 無理数を表す記号\(\sqrt{ルート}\)を根号（こんごう）といいます。 根号については教科書程度で十分理解できますので、 ここでは、みんながつまずきやすい点について少し触れてお解説 平方根で表された数の大小を比較するには、 例えば、 ＝約14、 ＝約24 などの近似値で表してみると簡単です。 このとき、 ＝約48、 ＝約84 などとなります。 分母に平方根があるものは、分母を有理化してから小数に直します。 例えば、 ＝約21 などです。この記号 $\ $ をガウス記号と呼ぶ ただし, この記法と呼称が通用するのは, 日本やドイツなど一部の地域に限られる 英語では, これを $\lfloor a\rfloor$ で表して, 関数 $\lfloor\ \rfloor$ を floor function

(1 t) 1 t の値は上の表よりある値に近づいていることがわかる．その値は，･････････の無理数となり e の記号をつかって表す． e = lim t → 0 (1 t) 1 t より， lim x → 0 log (1 x) x = 1 ⇒ 参照 lim x → 0 e x − 1 x = 1 ⇒ 参照 の関係式が得体を解説する前に数学で使う数の集合について，その記号を示す． 整数も含め，有理数，実数，複素数をあらわす集合は次のように表現されるのが一般的になっている． Z，整数(正負ともに，0 も入れた) 全体の集合 記号Zの由来は，ドイツ語で数を意味するZahlen かP 2 2 R n Q;

有理数と無理数の稠密性 高校数学の美しい物語

中3の数学 有理数 無理数 の問題でどうして キ は分数なのに無理数な Yahoo 知恵袋

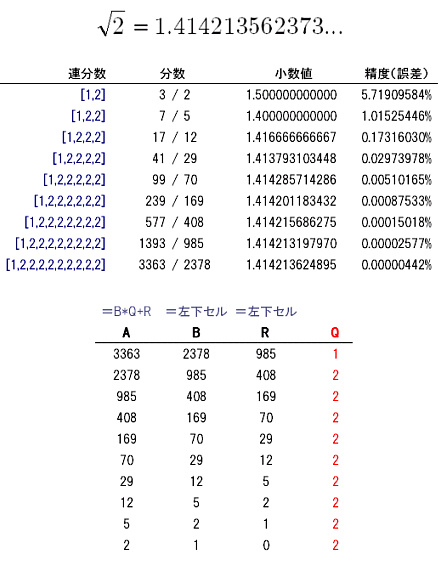
数でないとする．このとき， 𝑥2 𝑥 =0 の根を二次無理数という． さらに， 𝑥2 𝑥 =0の一つの解を𝜔とし，もう一つの解を𝜔′とするとき，𝜔′を𝜔の 共役解という． 定理3 無理数はただ一通りの正則連分数展開をも記号 n, z, q, r, cをそれぞれ自然数全体の集合，整数全体の集合，有理数全 体の集合，実数全体の集合，複素数全体の集合とする． 目次 1 ユークリッドの互除法 1 2 1次不定方程式 3 3 合同式 5 4 有理数 7 5 無理数 9 6 連分数 10 7 代数的数と超越数 16 8 円周率の無有理数と無理数 数を無理数と呼びます 無理数です ここに代表的な無理数を上げておきました パイという記号であらわされる円周率は無理数です 小数点以下が循環しないで無限に続きます 自然対数の底 e も小数点以下が循環しないで無限に続き

Lihat Cara Penyelesaian Di Qanda

実数とは 0 は実数 定義や記号 虚数との関係や計算方法 受験辞典

無理数（むりすう）とは、のように循環しない無限小数のことです。 逆に0333を循環する無限小数といいます。 0333は小数点以下に3が無限に続きます。 無理数でない実数が有理数です。 今回は無理数の意味、有理数との違い、0、π、循環小数との関係について説明します。 有理数、小数の意味は下記が参考になります。 有理数とは？ 1分でわかる · →無理数乗は有理数乗の極限で定義しよう という考え方です。 厳密には， 各項が有理数で x x x に収束する数列 x k ( k = 1 , 2 , ⋯ ) x_k\(k=1,2,\cdots) x k ( k = 1 , 2 , ⋯ ) を取ってきて， a x = lim ⁡ k → ∞ a x k a^x=\displaystyle\lim_{k\to\infty}a^{x_k} a x = k → ∞ lim a x k と定義します。数学用語と記号 2 Mproject 取り上げた用語と記号 数学、代数、幾何、解析、確率、群、環、体、束、コンピュータ、アルゴリズム 分数、逆数、小数、自然数、整数、有理数、無理数、実数、虚数、複素数、

数学基礎 素数のべき乗根が必ず無理数になることの証明 竜太のブログ

べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ

問題と考え方 上 条件と結論の分析 前 結論からさかのぼる 定義に立ちかえる 糸口がわからないとき，まず考えるべきことは，問題文中の言葉および記号の意味ははっきりわかっているか，ということである．そこをおさえることで解決の糸口がつかめることが少なくない．プラス記号とマイナス記号、正の数と負の数 算術 小数 、 分数 、 有理数 、 無理数 、 実数 、 虚数 、 複素数 、 四元数中3です。有理数と無理数の見分け方がいまいちわかりません。 なにかわかりやすい簡単な見分け方や、コツなどを教えていただきたいです。 / もし分数にして表現できる場合は有利数です。それ以外の数は無理数です。 平方根をとる（ルートに入れる）とき、ルート9＝3

大学数学 集合 数学 大学 に関する質問 勉強質問サイト

実数の意味と例 0 負の数 および実数でないものの例 具体例で学ぶ数学

16年10月23日 18年4月8日 ガウス記号と有理数、無理数の絡んだ問題です。 1． B (北海道大) 実数 に対し， 以下の整数のうちで最大のものを と書くことにする． として， とおく．以下を証明せよ． (1) すべての に対して， は または に等しい． (2) が有理数のときは， となる が存在する． (3) が無理数のときは，すべての に対して となる．2) 無理数は無限正則連分数で表せる．無限正則連分数は無理数を表す． 3) 2次無理数は，（無限）循環連分数で表せる．（無限）循環連分数は2次無理数を表す． （2次無理数とは，整数係数の既約2次方程式の解のこと）00 · 例えば、「以上から、√2は無理数である」と書くよりも、「∴√2∉q ∩√2∈ r」と書いた方が簡単だし、綺麗ですよね。 数式をより綺麗に・より簡単に書けるようになると、数学の問題を解くのがもっと楽しくなるので、ぜひこの記事で紹介した記号を実際に使ってみてくださいね。

無理数とは何ですか Clear

平方根の無理数と有理数の簡単な見分け方おしえてください 平方 Yahoo 知恵袋

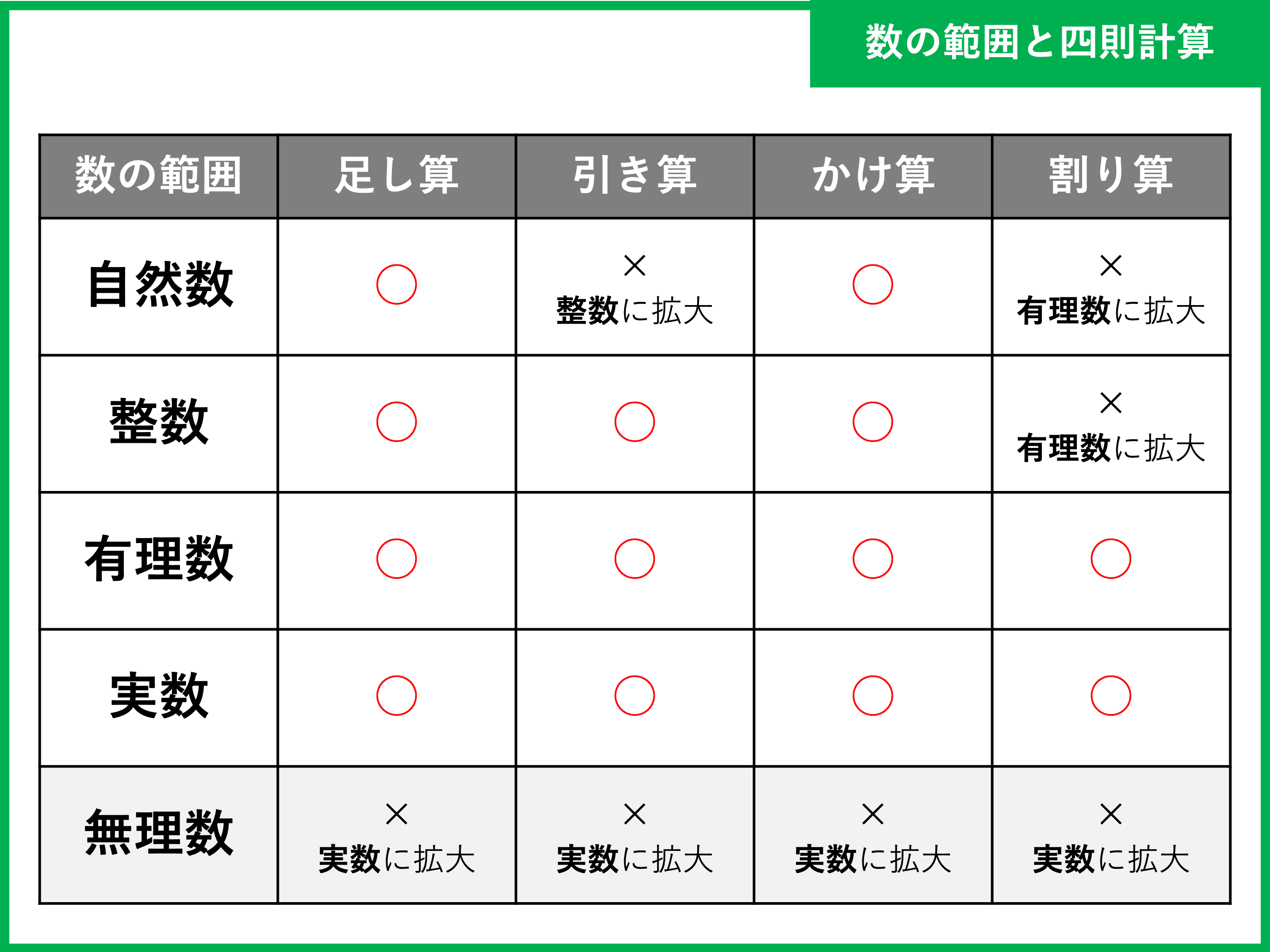
(3) 25は有理数ですか，無理数ですか。 25＝ だから 25は である。 2 数についてまとめると，下のような図になり ました。 に当てはまることばを入れなさい。 (p41) 3 下の数の中から，有理数と無理数を選び記号 で書きなさい。有理数では、分子と分母の両方が整数で、分母はゼロに等しくありません。 無理数は分数で書くことはできませんが。 有理数には、9、16、25などのような完全な正方形の数が含まれます。 一方、無理数には、2、3、5などのような余剰が含まれます。な無理数の四則計算をすること。 の集合を表しなさい。 ・自然数、整数、有理数、無理数の包含関係など、実数 の構成を理解する。 ・実数と直線上の点が一対一対応であることを理解し、 実数を数直線上に示すことができる。

有理数と無理数２ 有理数の稠密性を中心として 身勝手な主張

微分 無理数の指数 についてのイントロダクション 大人が学び直す数学

無理数全体の集合を表す標準的な記号はないようである。後で説明する差集合の記号n を 用いて、RnQ とするのが普通である。 例22 1 2 N, 1 ̸ N, 1 2 Z, 3 2 Z, 3 2 2 Q, ˇ ̸ Q, ˇ 2 R, 1 p 3i 2 R, 1 p 3i 2 2 C どんなa に対しても、a 2 A かa ̸ A か、はっきり定まっているの教科：数 学 科目：数学Ⅰ 作成様式 学習指導要領 大島海洋国際高校 学力スタンダード (1) 数 と 式 ア 数と集合 （ア）実数 数を実数まで拡張する意義を理解し、簡単 な無理数の四則計算をすること。 の集合を表しなさい。本書では, 自然数全体の集合, 整数全体の集合などを良く用いる これらの 集合は, 次にあげる記号で表されるのが一般的である 但し, 次式において " def= " とは左辺を右辺として定義(definition) するという意味である Ndef= 自然数(natural number) 全体の集合

ねこ Na Twitteru 1のみを要素にもつ集合は有理数全体の集合aの部分集合である という中身がまるでない真の命題を 記号を用いて表せ

実数とは 0 は実数 定義や記号 虚数との関係や計算方法 受験辞典

P 1 2 C n R R n Q 無理数全体の集合 2Amazonで一松信の√2の数学―無理数を見直す (Monad books)。アマゾンならポイント還元本が多数。一松信作品ほか、お急ぎ便対象商品は当日お届けも可能。また√2の数学―無理数を見直す (Monad books)もアマゾン配送商品なら通常配送無料。Mixi背理･逆説･パラドックス 辿りつけない無理数 πとか、ルート2とかは無理数と呼ばれていますが、こういった無理数というのは現実に存在しているのかどうかという議論があるといったことを本で読みました。 確かに、無理数πについて考えてみると、永久に（小

円周率の日のカラフルな水平方向のバナーのセット 円周率のギリシャ文字 無理数数学定数 P 記号番号 デジタル ベクトル図を抽象化します のイラスト素材 ベクタ Image

Pi 記号数学定数無理数ギリシャ文字パターン背景中心 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

中学数学では有理数と無理数の違いについて学びます。ルートは無理数の代表例であるため、平方根を学ぶときに無理数を習うのが一般的です。数学では、分数で表せない数字として無理数があることを理解しましょう。 練習問題：平方根の計算 q1 次の数（かず、すう、英 number ）とは、 ものの順序を示す語 。 また、その記号 、数字 。; · という信条を持っていたため、 \(~\sqrt{2}~\) という無理数を認めず、平方根という概念や記号など考えもしませんでした。 ※この信条に反したピタゴラス教団の若者が溺死させられるといった事件まで発生するほど、無理数を認めようとしませんでした。

数学 使用する記号は決まっているのか 記号一覧 もう一人のy君

6 1 Lihat Cara Penyelesaian Di Qanda

Q 有理数全体の集合 R 実数全体の集合 C 複素数全体の集合 ただし，書籍等ではN;Z;Q;R;C などのボールド体が使われることが多い． 使用例 1 2 N ˆ Z ˆ Q ˆ R ˆ C 1 2 Z n N;その一部であるPisot 数系とそれに 付随するタイル張りを中心に諸結果を解説する 1 スツルム列と記号力学系 非周期的な対象は数学的扱いが難しく統一的理論が出来ないことが多 い 例外的にスツルム列には一次元無理回転と結びつける理論が構築さ れている数学・算数 無理数が分子、有理数が分母の分数は無理数ですか 分子、分母ともに無理数の場合は必ず有理数になりますか。 質問No

Pi 記号数学定数無理数ギリシャ文字背景 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

実数とは何かを即理解 試験で使えるテクニックとは 高校生向け受験応援メディア 受験のミカタ

63 平方根の記号 $\sqrt{\mathstrut \quad}$ はrootの頭文字 $r$ の変形 7．無理数は不合理な数か 71 無理数は無比数と訳すべきだった 72 ギリシア時代から $\sqrt{\mathstrut \;2\;}$ は不合理な数だった

49 0 3 0 01 3分の 16 13分の 169が有理数な理由と Clear

有理数 無理数とは 定義や具体例 違いと見分け方 証明問題 受験辞典

Pi 記号数学定数無理数ギリシャ文字背景 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

この問題の答えはアです どうして 有理数と有理数の積は有理数 と分かるんですか Clear

数と式 平方根について 日々是鍛錬 ひびこれたんれん

数と式 絶対値を扱った問題を解いてみよう 日々是鍛錬 ひびこれたんれん

どうして 7分の3が無理数になるのかわからないです ᐪᐤᐪ Clear

絶対値と場合分け 数学 苦手解決q A 進研ゼミ高校講座

数学塾直伝 今度こそs シグマ 記号を攻略しよう 公式の図解と証明 年5月8日更新 永野裕之のblog

実数とは 1分でわかる意味 定義 0 分数 小数 虚数との関係

微分 無理数の指数 についてのイントロダクション 大人が学び直す数学

2 Pi Lihat Cara Penyelesaian Di Qanda

75 パイ の 記号 画像ブログ

集合

実数とは 0 は実数 定義や記号 虚数との関係や計算方法 受験辞典

数の構成 連分数と無理数 大人が学び直す数学

自然数 整数 有理数 実数 複素数の定義と関係性

数 有理数 の復習 自由に 身勝手な主張

有理数と無理数 中学数学に関する質問 勉強質問サイト

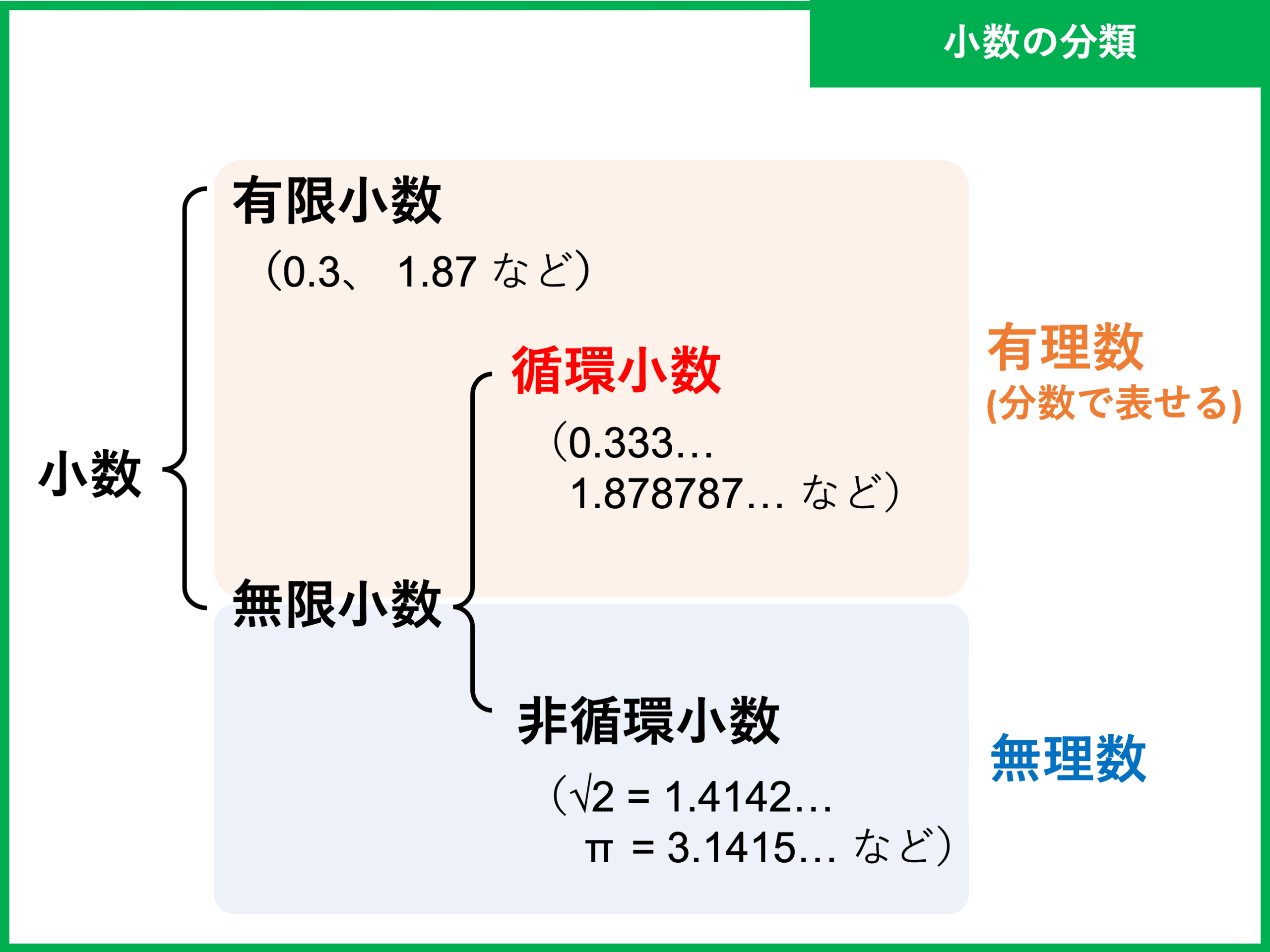
循環小数とは 分数に直す方法や記号による表し方 計算問題 受験辞典

Pi 記号数学定数無理数ギリシャ文字パターン背景中心 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

4 で 2枚目の の部分で何をしてるのかわからないのですが Clear

有理数と無理数の稠密性 高校数学の美しい物語

数学塾直伝 平方数 立方数 無理数の覚え方 語呂合わせ 永野裕之のblog

有理数 無理数とは 定義や具体例 違いと見分け方 証明問題 受験辞典

円周率とラマヌジャン Qiita

次の数のうち 有理数と無理数をそれぞれすべて記号で答えよ Yahoo 知恵袋

7 Sqrt26 I Sqrt400 Lihat Cara Penyelesaian Di Qanda

白の背景にベクトル黄金キラキラ Pi 数です円周率の記号数学定数無理数ギリシャ文字抽象的なデジタル イラスト装飾のデザイン要素です イラストレーションのベクターアート素材や画像を多数ご用意 Istock

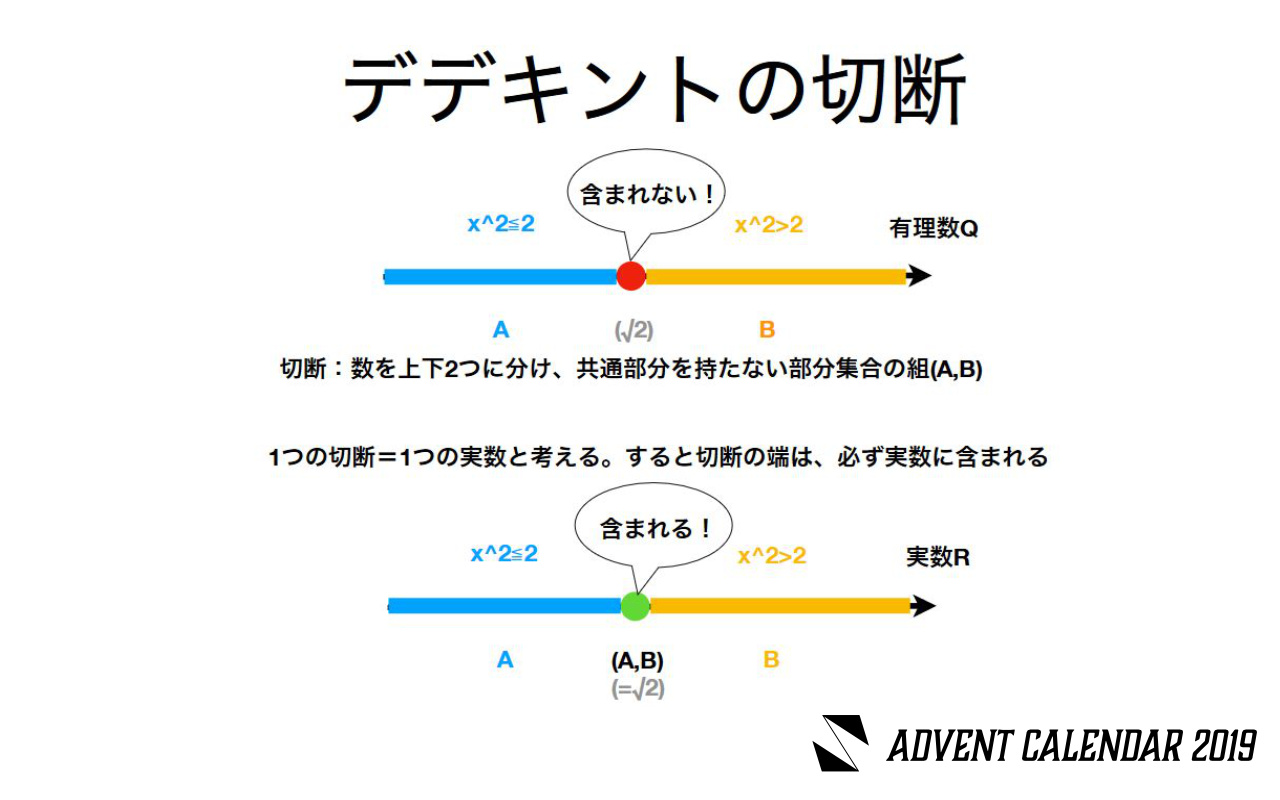
数を 作って みよう 近代数学と数概念の自由さについて Share Study

有理数 無理 数 違い Article

Pi 記号数学定数無理数ギリシャ文字パターン背景中心 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

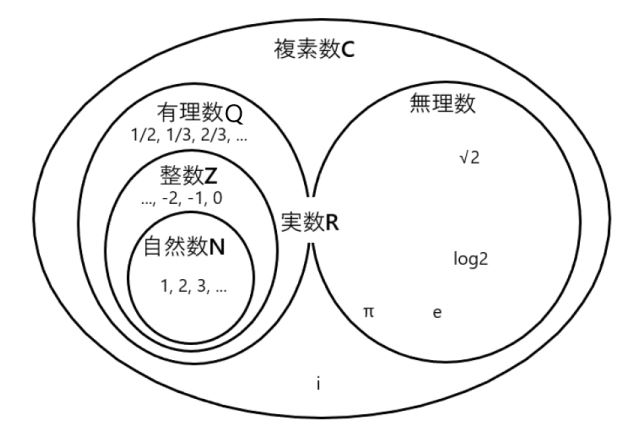
自然数 整数 有理数 実数 複素数の定義と関係性

Pi 記号数学定数無理数ギリシャ文字背景 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

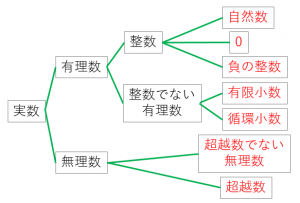
自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ

自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ

ニアリーイコール の使い方と記号入力の出し方について アタリマエ

数学 自然数 整数 有理数 無理数 実数 複素数 もう一人のy君

Sqrtdfrac94 Sqrt081 Lihat Cara Penyelesaian Di Qanda

これの解説お願いしたいです 答え あ 1 A ア 4 Clear

有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun

こーちゃん 厳密に無理数かどうか判断するには背理法が必要って観点では確かに

Ios端末における消失個所のサポート 下に 現時点でこちらで確認した消失個所のページ画像一覧を載せておきます 必要に応じてご覧ください ただ かなり深刻なバグがあるようで 消失していた部分が忽然と現れることもあるようです つまりその逆

実数とは 0 は実数 定義や記号 虚数との関係や計算方法 受験辞典

楽天ブックス 数学1 A標準問題精講 麻生雅久 本

5 ガウス記号などの新記号問題 京極一樹の数学塾

Pi 記号数学定数無理数ギリシャ文字パターン背景中心 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

P 記号の付いたカラフルなフラット アイコンをセットします 数学定数 無理数 ギリシャ文字 円周率の日の抽象的なベクトル イラスト のイラスト素材 ベクタ Image

数学i 怜悧玲瓏 高校数学を天空から俯瞰する

実数とは何かを即理解 試験で使えるテクニックとは 高校生向け受験応援メディア 受験のミカタ

白い背景に影で円周率を青します 円周率の記号 数学定数 無理数 ギリシャ文字 デジタル ベクトル図を抽象化します のイラスト素材 ベクタ Image

実数とは何かを即理解 試験で使えるテクニックとは 高校生向け受験応援メディア 受験のミカタ

根号をふくむ式の計算の仕方がわかりません おしえてください 中学3年 Clear

共通テスト試行調査の という命題を 記号を用いて表せ は出題ミスなのか Togetter

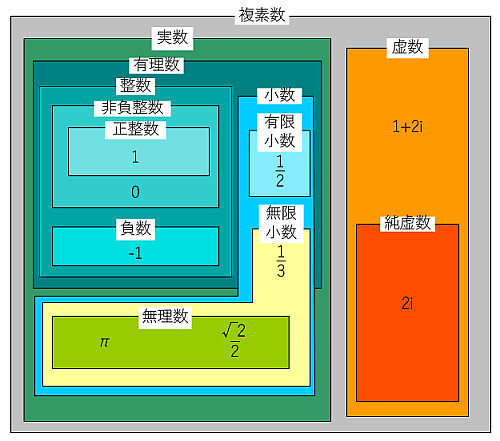
数学 自然数 整数 有理数 無理数 実数 複素数 もう一人のy君

有理数と無理数 中学数学に関する質問 勉強質問サイト

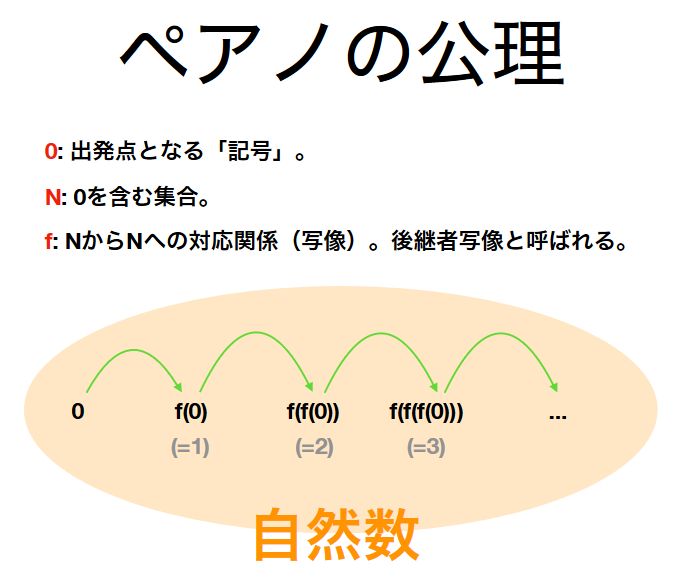
数を 作って みよう 近代数学と数概念の自由さについて Share Study

0sqrt49 0 Dfracsqrt25 Dfr Lihat Cara Penyelesaian Di Qanda

ガウス記号の問題です A Bを1 A 1 B 1をみたす正の無理数 Yahoo 知恵袋

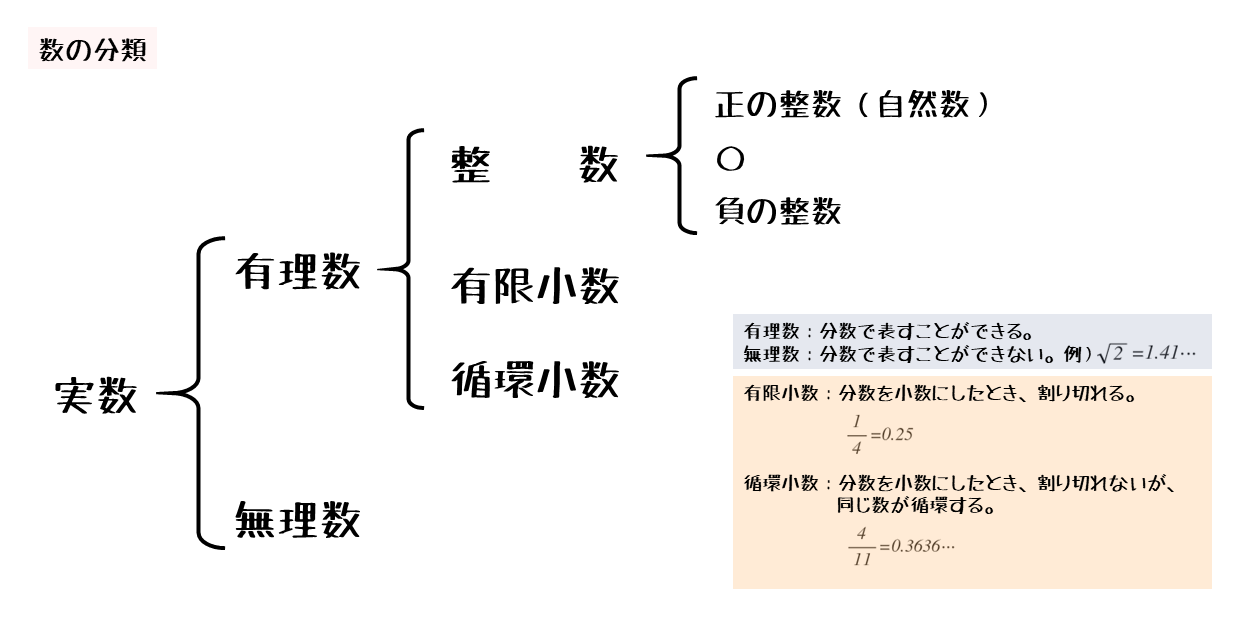
数と式 数の定義について 日々是鍛錬 ひびこれたんれん

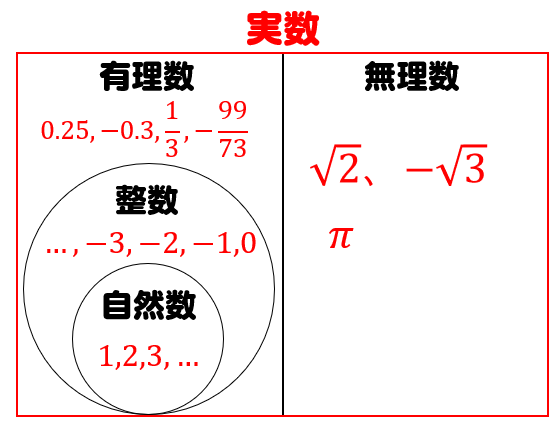
有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun

Pi 記号数学定数無理数ギリシャ文字パターン背景中心 イラストレーションのベクターアート素材や画像を多数ご用意 Istock

再考数学用語 無理数は何が無理なのか Sakurai Susumu Website

数学塾直伝 平方数 立方数 無理数の覚え方 語呂合わせ 永野裕之のblog

いろいろな数 数学i フリー教材開発コミュニティ Ftext

無理数 Wikipedia

平方根 有理数と無理数 清水塾

有理数 無理数とは 定義や具体例 違いと見分け方 証明問題 受験辞典

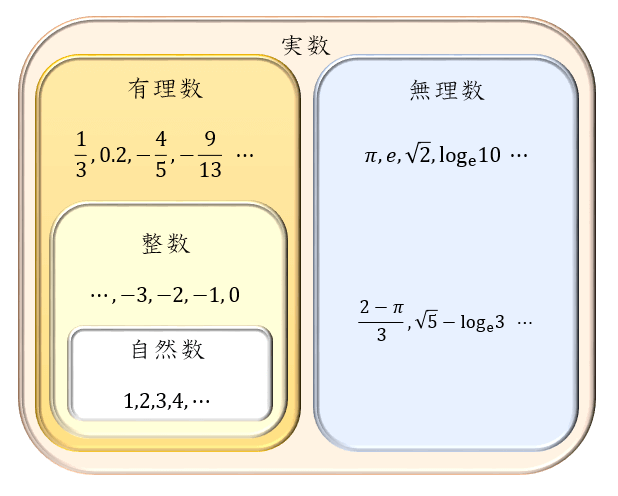
自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ

Incoming Term: 無理数 記号, 有理数 無理数 記号,